Rotating Reference Frames

 

Let the X-Y coordinate system be inertial and fixed and the x-y coordinate system be a body-fixed coordinate system that may translate and rotate as shown in the figure.

 

 

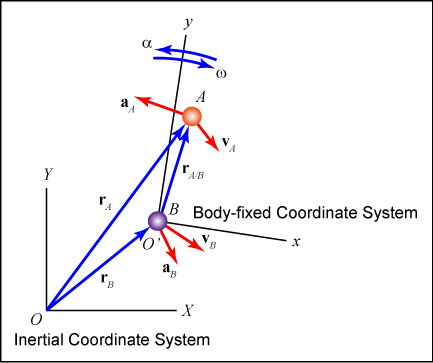
If the x-y coordinate system translates and rotates, the derivatives of the unit-direction vectors may not equal zero. This fact provides different equations for a particle's velocity and acceleration in terms of the rotating reference frame.

 

• Position: r_A = r_B + r_A/B = r_B + (xi + yj)

 

• Velocity: v_A = v_B + v_A/B = v_B + v_A,rel + ω x r_A/B

 

• Acceleration: a_B = a_B + a_A/B = a_B + a_A,rel + α x r_A/B - ω_CD² r_B/C + 2ω x v_A,rel