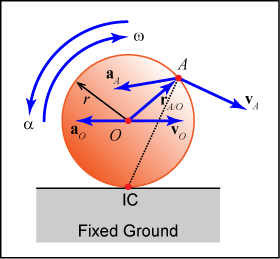
Instantaneous Center of Zero and Known Velocities
Rolling
Rolling is a special type of rigid body general planar motion. It occurs so frequently that it deserves a special look. There are two cases of rolling; rolling without slip and rolling with slip.
What is the difference between a wheel that rolls without slip and one that rolls with slip?
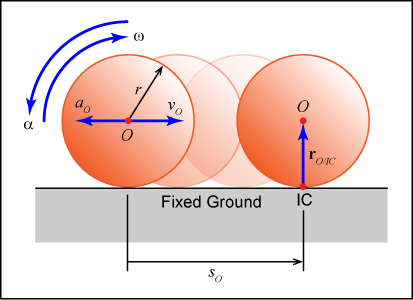
In the case where we have rolling without slip, imagine that a rope is wrapped around the circumference of the body. As the body rolls, this rope is unwound and laid upon the ground. The length of rope laid down represents the displacement of the body's center (sO) as shown in the animation.
If a wheel rolls without slip, the equations that govern its motion are ...
- Distance traveled by the wheel's center: sO = rθ
- Velocity of the wheel's center: vO = rω
- Acceleration of the wheel's center: aO = rα
Once the motion of the wheel's center is determined, any point on the body may be analyzed.
- Velocity of a point on the wheel: vA = vO + vA/O = vO + ω x rA/O
- Acceleration of a point on the wheel: aA = aO + aA/O = aO + α x rA/O - ω2rA/O